Le jardin de Pythagore

Préambule

C’est la troisième et dernière année que je participe àl’atelier MATh.en.JEANS, pour ceux qui ne connaissent pas l’atelier, je le décris brièvement ici.

Cette année, compte tenu des circonstances actuelles, le congrès n’a évidemment pas eu lieu, ce qui ne nous a pas empêché de publier le rendu de nos recherches. Comme ce fut le cas l’anée dernière, nous avons été suivi par le chercheur Charles Dossal qui nous a de nouveau proposé trois sujets :

• « Le jardin de Pythagore »
• « Un jeu d’allumettes »
• « Un tour de cartes »

Comme le titre de la page l’indique, c’est du côté de Pythagore que je suis partie…

Présentation du problème

Pythagore était un philosophe et mathématicien grec qui aurait vécu vers 550 avant J-C. Pendant sa vie, il se découvrit une passion pour les nombres entiers. Aussi, lorsqu’il voulut placer des statues dans son jardin qui était aussi vaste que l’on souhaite, il décida que toutes les distances entre deux statues devraient être des nombres entiers de pas, et que toutes les statues ne devraient pas être alignées. Comment peut-on aider Pythagore à trouver des dispositions dans lesquelles il y a le plus de statues possibles ?

Remarque : On considérera pour la suite qu’un pas correspond à une distance d’un mètre, et que trois statues ne seront jamais alignées.

Approche numérique

Le premier réflexe consiste à chercher des configurations qui contiennent de plus en plus de points, seulement ce travail devient rapidement laborieux et bien souvent n’aboutit pas. L’idée est donc, grâce à un programme, de trouver de tels placements et d’en déduire une logique, une façon d’ordonner les statues maximisant leur nombre. Le programme en question a été réalisé en python avec la distribution anaconda et l’environnement de développement spyder.

Le fonctionnement global est le suivant :

• On se donne deux points et on repère tous ceux qui s’y trouvent à une distance entière
• A partir des coordonnées obtenues on créé des groupes de points à distance entière les uns des autres, vérifiant le « non-alignement » imposé
• On sélectionne les plus grands, on enregistre leurs coordonnées puis on trace les résultats obtenus.

Repérage des points

Le but étant de récupérer les coordonnées des points à une distance entière des deux initiaux ($A$ et $B$), on procède en traçant des cercles de rayons croissants : $1, 2, \ldots, p$ ayant pour centre $A$ et $B$.

Pour chaque intersection de deux cercles, on est ainsi assuré que le point est à une distance entière de $A$ et de $B$.

En voici une illustration avec $p = 5$ cercles :

Simplifications des paramètres

Le but est donc de récupérer les coordonnées de chaque point d’intersection entre deux cercles. Pour cela, nous allons créer une fonction permettant de calculer les dites intersections connaissant les coordonnées de $A$ et $B$ et les rayons des deux cercles. Mais avant, remarquons que quelques paramètres se simplifient :

• Tout d’abord, observons $A$ et $B$, on remarque que seule la distance qui les sépare influe sur le résultat : l’orientation de la droite passant par ces deux points (par rapport à l’axe des abscisses par exemple) ne change en rien les résultats. Ainsi, au lieu de rentrer comme paramètres $A(x_A , y_A)$ et $B(x_B , y_B)$ on peut choisir arbitrairement $y_A = y_B = 0$ ce qui permet de simplifier considérablement les prochains calculs.
• De la même manière, on peut fixer $A$ sur l’axe des abscisses la distance pouvant être modifiée en faisant varier l’abscisse de $B$. Ainsi on peut prendre $x_A = 0$ et donc $x_B = d$ où $d$ est l’écartement entre $A$ et $B$.
• Puisque $A$ et $B$ sont sur l’axe des abscisses, les coordonnées d’intersection entre deux cercles seront symétrique par rapport à cet axe : soit il n’y a pas de solutions, soit il y a une unique intersection placée sur l’axe des abscisses (cercles tangents) mais qui ne nous intéresse pas car le point en question serait aligné avec $A$ et $B$, or on a exclu cette possibilité. Soit il y a deux points d’intersection dont l’un est déductible de l’autre : on se limitera donc à l’étude des points ayant une ordonnée positive.
• Enfin, en posant $r_1$ le rayon du cercle de centre $A$ et $r_2$ le rayon du cercle de centre $B$, on peut supposer $r_1 > r_2$. En effet, dans le cas contraire il nous suffira d’avoir recours à une symétrie axiale par rapport à la droite $x = \frac{d}{2}$

Voici un exemple illustrant ces simplifications :

Calcul des intersections entre deux cercles

Les simplifications précédentes nous ont apporté $A(0,0)$, et $B(d,0)$ ainsi que $r_1 > r_2$.

Les équations des deux cercles sont donc :

\begin{eqnarray}
x^2 + y^2 = r_1^2 \
(x – d)^2 + y^2 = r_2^2
\end{eqnarray}

Avec $(1)$ on obtient (on a de façon évidente $|x| \leq r_1$) :

\begin{eqnarray}
y = \sqrt{r_1^2 – x^2}
\end{eqnarray}

Et en combinant avec la $(2)$ on a finalement :

\begin{eqnarray}
\begin{cases}
x = \dfrac{d^2 + r_1^2 – r_2^2}{2d} \
y = \sqrt{r_1^2 – x^2}
\end{cases}
\end{eqnarray}

Calcul de toutes les intersections

On a, à présent, une fonction permettant de calculer les éventuelles intersections entre deux cercles. Il reste à l’appliquer à notre problème, et pour ce faire, il convient d’étudier trois configurations :

• Si $r_1 + r_2 < d$, les cercles ne s’intersectent pas ($B_2$ sur la figure): il n’y a donc pas de points à retourner. On peut éliminer ce cas.
• Si $r_1 + r_2 = d$, comme vu précédemment les cercles sont tangents en $y = 0$, ils ne nous intéressent donc pas.
• Si $r_1 > r_2 + d$, le cercle de centre $A$ englobe celui de centre $B$ ($B_1$ sur la figure) : il n’y a donc pas de points d’intersection.

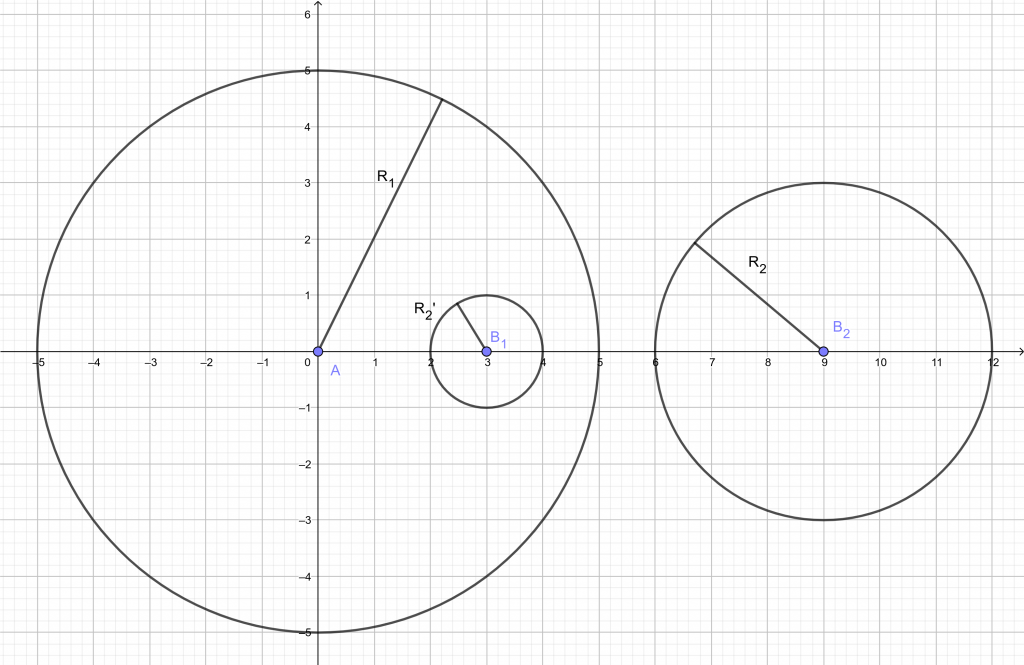
Sorti de ces trois cas de figure, la fonction établie nous retournera un unique couple $(x, y)$.

Il nous suffit donc d’enregistrer les points d’intersection pour $r_1$ allant de $1$ à $p$ et $r_2$ allant de $1$ à $r_1$ (puisque $r_1 > r_2$) dans une liste.

Prise en compte des symétriques

La dernière étape consiste à intégrer les symétriques à notre liste. Premièrement, ceux par rapport à l’axe des abscisses, pour cela on a vu que pour chaque point de la liste il suffit de rajouter ce même point en opposant son ordonnée. Deuxièmement, ceux par rapport à l’axe $x = \frac{d}{2}$, il suffit donc, pour chaque point de modifier son abscisse $x$ en $d – x$. Ainsi, on obtient une grande liste contenant tous les points à une distance entière de $A$ et $B$ (inférieure à $p$).

Enregistrer l’information

Matrices et matrices creuses

Pour trouver un maximum de points à distances entières les uns des autres on pourrait raisonner en listes imbriquées, mais le programme qui en découlerait serait infiniment long. Pour éviter cela, on va utiliser des matrices uniquement remplies de $0$ et de $1$, ayant $n$ lignes et $n$ colonnes où $n$ représente le nombre d’intersections (longueur de notre liste). L’intersection de la ligne $i$ et de la colonne $j$ vaut $1$ si les deux points correspondant sont à une distance entière, $0$ sinon.

Remarque : On considérera pour la suite qu’un pas correspond à une distance d’un mètre, et que trois statues ne seront jamais alignées.

On obtient finalement une matrice énorme avec quelques $1$ et une grande majorité de $0$. C’est donc une matrice très gourmande en stockage qui, en plus, doit être stockée plusieurs fois (il faudra bien évidemment lui apporter des modifications..). Pour un nombre de cercles trop élevé, l’ordinateur plante. Il s’agit donc de trouver un nouveau moyen de stockage beaucoup plus léger. Une remarque importante est le fait que notre matrice est essentiellement composée de $0$ : on appelle une telle matrice une matrice creuse ou sparse matrix en anglais.

Une façon de stocker intéressante serait donc de n’enregistrer que les $1$ : pour ce faire il suffit de les repérer par leur ligne et leur colonne puis d’enregistrer ces informations dans des listes.

Voyons de plus près ce fonctionnement :

Toutes les informations sont rentrées dans trois listes,

• Une liste $A$ qui contient les valeurs de tous les éléments non nuls. Dans notre cas, elle ne contiendra que des $1$,
• Une liste $I$ indiquant, ligne après ligne, les colonnes où sont contenues les $1$,
• Une liste $J$, fonctionnant aussi ligne après ligne, renseigne sur le nombre de valeurs non nulles sur chaque ligne.

Remarque : La première ligne et la première colonne sont d’indice $0$.

Considérons l’exemple suivant :

$$
\begin{pmatrix}
1 & 0 & 2 & 3 \
0 & 4 & 5 & 0 \
6 & 7 & 8 & 0 \
0 & 0 & 0 & 9
\end{pmatrix}
$$

• La liste $A$ contient les valeurs de ses éléments non nuls à savoir $A = [1, 2, 3, 4, 5, 6, 7, 8, 9]$, pris en parcourant les lignes.
• La liste $I$ indique les indices des colonnes où sont placés les éléments, donc $I = [0, 2, 3, 1, 2, 0, 1, 2, 3]$. Avec ces deux listes seulement, on sait déjà que la valeur $1$ sera sur la colonne $0$, la valeur $2$ sur la colonne $2$, $\ldots$, la valeur $9$ sur la colonne $3$.
• Enfin, $J = [0, 0, 0, 1, 1, 2, 2, 2, 3]$.

Dès lors, chaque élément est parfaitement déterminé par sa valeur ($A$), sa colonne ($I$), sa ligne ($J$) et il nous suffit de stocker $3n$ informations au lieu de $n^2$ ce qui fait une énorme différence.

Permutation inter-matricielle

Les trois listes obtenues sont ensuite renseignées dans la fonction csr_matrix((data, (row, col)), shape=(n, n)) (le package utilisé vient de la bibliothèque \textit{scipy sparse}) où data correspond à $A$, row à $J$ et col à $I$, celle-ci stocke la matrice sous une forme encore autre dont on reparlera plus tard.

La matrice stockée, il faut maintenant trouver un moyen de l’exploiter ce qui risque de s’avérer difficile étant donné la faible proportion de $1$. On aimerait donc pouvoir les rassembler : pour cela, une solution envisageable est de les rapprocher de la diagonale en permutant des lignes et colonnes de la matrice. C’est ce que propose la fonction reverse_cuthill_mckee(graph, symmetric mode) dont le seul paramètre est la matrice mais on peut aussi activer ou non la symétrie de la matrice permutée, dans notre cas on va évidemment l’utiliser. Cette fonction sort une liste des permutations des lignes et colonnes à effectuer.

Dans l’exemple précédent, si la liste de permutation obtenue était $perm = [3, 2, 0, 1]$ cela signifierait que la colonne et la ligne d’indice $3$ de la matrice se trouverait en position $0$ dans la nouvelle, celles de rang $2$ en $1$, etc.

A ce niveau là, il faut trouver comme permuter les lignes et colonnes de notre matrice. Pour cela, procédons comme suit :

On créé une matrice permutation composée de un seul $1$ sur chaque ligne et colonne qui, multipliée à notre matrice initiale, permute les lignes. On la construit ainsi :On créé une matrice permutation composée de un seul $1$ sur chaque ligne et colonne qui, multipliée à notre matrice initiale, permute les lignes. On la construit ainsi :

• data $ = [1, 1, \ldots, 1]$ avec $n$ occurrences de $1$
• row $= [0,1, 2, \ldots, n]$ (un $1$ sur chaque ligne)
• col $=$ liste permutation

Par exemple, si l’on souhaite permuter notre « matrice exemple » telle que $ perm = [3, 2, 0, 1]$, la « matrice permutation » serait :

$$
\begin{pmatrix}
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
\end{pmatrix}
$$

Et en lui multipliant la matrice initiale on obtient :

$$
\begin{pmatrix}
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
\end{pmatrix}
\times
\begin{pmatrix}
1 & 0 & 2 & 3 \\
0 & 4 & 5 & 0 \\
6 & 7 & 8 & 0 \\
0 & 0 & 0 & 9 \\
\end{pmatrix}
$$

$$
=
\begin{pmatrix}
0 & 0 & 0 & 9 \\
6 & 7 & 8 & 0 \\
1 & 0 & 2 & 3 \\
0 & 4 & 5 & 0 \\
\end{pmatrix}
$$

Ce qui correspond bien à une permutation des lignes.

On construit la matrice transposée de notre matrice permutation (symétrie par rapport à la diagonale), il existe là encore une fonction préconçue : csr_matrix.transpose(matrice permutation).

Dans notre cas on obtient la matrice suivante :

$$
\begin{pmatrix}
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
\end{pmatrix}
$$

Que l’on multiplie à la matrice précédemment obtenue :

$$
\begin{pmatrix}
0 & 0 & 0 & 9 \\
6 & 7 & 8 & 0 \\
1 & 0 & 2 & 3 \\
0 & 4 & 5 & 0 \\
\end{pmatrix}
\times
\begin{pmatrix}
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
\end{pmatrix}
$$

$$
\begin{pmatrix}
9 & 0 & 0 & 0 \\
0 & 8 & 6 & 7 \\
3 & 2 & 1 & 0 \\
0 & 5 & 0 & 4 \\
\end{pmatrix}
$$

On a ainsi créé la matrice permutée souhaitée.

Retenons que si on appelle $A$ la matrice initiale, $B$ la matrice permutation, $B^T$ la transposée de $B$ et $D$ la matrice finale, alors on a la relation :

\begin{equation}
B\times A \times B^T = A’
\end{equation}

qui nous permet d’obtenir une matrice dans laquelle les $1$ sont rapprochés de la diagonale (elle même constituée de $1$, d’où l’intérêt de ne pas la remplir de $0$). Voici le résultat :

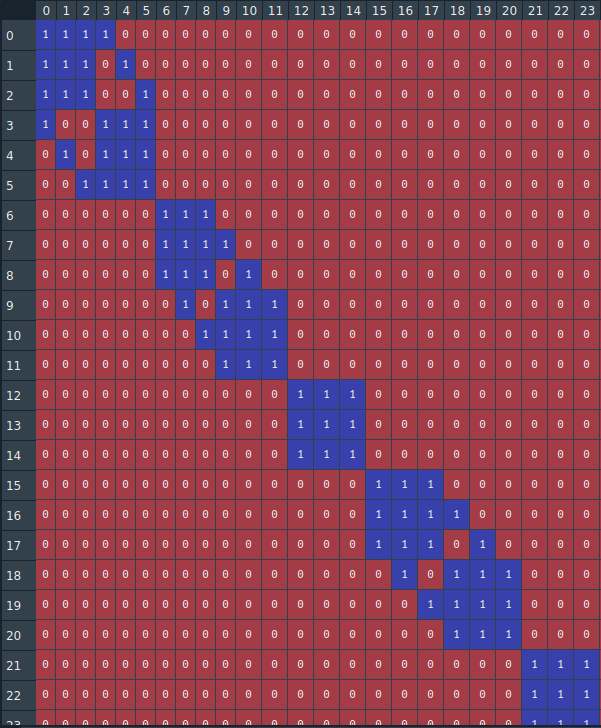
Traiter l’information

Subdivision en sous graphes

Cette représentation des choses semble effectivement beaucoup plus facilement exploitable que la précédente. On remarque d’ailleurs que les points sont regroupés en « paquets » isolés les uns des autres. En effet, de la ligne $5$ à $6$ par exemple on a un changement de « paquet », concrètement cela signifie que les points des lignes et colonnes de $0$ à $5$ n’ont pas de distances entières avec d’autres points : ils forment une sorte de sous-graphe. Ainsi, au lieu d’étudier notre matrice dans son entièreté, on peut étudier sous-graphe par sous-graphe ce qui réduit considérablement les possibilités.

Un sous-graphe est caractérisé par le fait qu’il est connecté au suivant et au précédent par un coin seulement, ainsi, pour les identifier, nous avons besoin des listes $I$ et $J$ qui renseignent sur la position des $1$. Seulement, nous avions évoqué le fait que la matrice n’était pas stockée grâce à ces listes, on ne peut donc pas y avoir accès. En effet, elle est stockée à l’aide des listes \textit{indptr} et \textit{indices} (et \textit{data} évidemment). Voyons à quoi cela correspond :

• indices est le plus évident puisqu’il correspond à notre liste $I$, soit l’index des colonnes
• indptr numérote toutes les valeurs non nulles de $1$ à $k$ (toujours en parcourant les lignes). Il enregistre ensuite l’index du dernier élément non nul de chaque ligne. \footnote{Si une ligne ne comporte que des $0$, dans ce cas il enregistre une seconde fois la dernière valeur trouvée, mais cette configuration n’apparaît pas dans notre cas puisque chaque ligne comporte au moins un $1$ (diagonale)}

Ainsi, on peut recréer la liste $J$ ou row : en effet, si entre l’élément $i$ et $i+1$ de la liste indptr il y a un écart de $k$ alors on sait qu’il y a $k$ éléments sur la ligne $i+1$. On peut donc construire à l’aide d’une boucle la liste souhaitée.

Revenons-en à la séparation des sous-graphe, il faut identifier les cas lors desquels les $1$ de deux lignes consécutives ne se touchent que par un coin, c’est-à-dire que si l’on se place sur le $1$ de la diagonale sur la ligne $i$ le prochain $1$ doit se trouver sur la ligne suivante, si tel est le cas, puisque la matrice est symétrique, on aura bien identifié deux graphes. Enfin, on enregistre dans une liste que l’on va nommer « position » les indices des lignes où débutent le nouveau graphe, sans oublier de rajouter $0$ pour le premier et $n+1$ pour le dernier.

Analyse des sous-graphes

On rentre maintenant dans une grande boucle, qui va permettre d’explorer tous les sous-graphes.

Leur taille est donnée en soustrayant la valeur de l’élément d’indice $k$ à celle d’indice $k+1$ dans la liste « position ». On peut dès lors décider de ne s’intéresser qu’au graphe ayant plus de $6$ points (la grande majorité n’en ayant qu’un, ça permet d’éliminer les cas inintéressants).

L’exploitation se fait en plusieurs parties :

1. Isolation d’un graphe : Grâce à la liste « position » on sait à quelle ligne commence la graphe et à laquelle il se finit, grâce à indptr on connaît l’indice du premier élément du graphe ainsi que le dernier : on a juste à récupérer dans nos listes $A$, $I$ et $J$ (data, row, et col), la séquence correspondante. A partir de ces données on peut créer le sous-graphe, et donc l’isoler.
2. Reconnaissance des cliques :  Une fois ce travail effectué, il reste des $0$ dans notre graphe. Il s’agit donc de trouver un sous-graphe ne contenant que des $1$, à savoir une clique ou encore un graphe complet. Pour cela il existe une fonction dans la bibliothèque numpy (find_cliques) qui permet de trouver les cliques maximales, soit les sous-graphes complets qui ne peuvent être agrandis. On ne sélectionne que les cliques excédant une certaine taille, $9$ par exemple. Une telle clique signifie qu’il existe $9$ points à distances entières les uns des autres : il reste à trouver lesquels.
3. Localisation des points : Enfin, une fois les cliques obtenues, il faut remonter le programme pour déterminer quels sont les points correspondant aux solutions trouvées. Pour cela, on repère la colonne de la clique trouvée, mettons $c$, or c’est celle obtenue après la permutation, donc la colonne initiale était col = perm[$c$]. Il suffit ensuite de chercher dans la liste de tous les points celui qui arrive en col \textit{ième} position. On peut ainsi retrouver les points correspondant aux sommets de nos graphes complets

Les résultats obtenus sont loin d’être surprenants : tous les points sont alignés sauf un ou deux. Ce n’est pas intéressant, on décide donc de se restreindre au cas où $3$ points ne sont jamais alignés, il faut donc trier les résultats obtenus.

Supprimer les points alignés

Le principe est simple : pour chaque paire de points du graphe complet, on calcule son équation de droite. Si un autre point se trouve sur cette droite alors il y a au moins $3$ points alignés donc ça ne nous intéresse pas. Il s’agit donc de calculer l’équation d’une droite passant par deux points.

Soit A($x_A, y_A$) et B($x_B, y_B$) deux points. La droite $d$ passant par ces deux points a pour équation :

\begin{equation}
d : -bx + ay + bx_A – ay_A = 0
\end{equation}
avec $a = x_B – x_A$ et $b = y_B – y_A$

Preuve :

Soit $M (x, y)$ un point de $d$,
Soit le vecteur $\overrightarrow{AB}(x_B -x_A, y_B – y_A)$ et le vecteur $\overrightarrow{AM}(x -x_A, y – y_A)$

Les deux vecteurs sont colinéaires, on en déduit qu’il existe $k$ appartenant aux réels tel que $\overrightarrow{AM} = k \times \overrightarrow{AB}$ d’où :

\begin{eqnarray}
\begin{cases}
x – x_A = k(x_B – x_A) \\
y – y_A = k(y_B – y_A)
\end{cases}
\end{eqnarray}

En posant $a = x_B – x_A$ et $b = y_B – y_A$, on obtient :

\begin{eqnarray}
\begin{cases}
x – x_A = ak  \\
y – y_A = bk
\end{cases}
\end{eqnarray}

D’où $b(x-x_A) = a(y – y_A)$ et ainsi $-bx + ay + bx_A – ay_A = 0$. $\blacksquare$

Ainsi, il suffit d’imbriquer des boucles pour parcourir les points de chaque clique, s’il existe un point $M$ tel que l’équation soit vérifiée alors la clique est supprimée et on passe à la suivante.

Une fois cet algorithme fini, on obtient un nombre restreint de cliques dont tous les points sont à distance entière les uns des autres et tels que trois d’entre eux ne sont jamais alignés. L’objectif est atteint.

Exploitation

Résultats

Après avoir fait tourner le programme pour une distance initiale entière variant de $5$ à $400$ et pour un nombre de cercle de $200$, on obtient finalement :

• $4$ graphes à $12$ points
• $0$ à $11$ points
• $15$ à $10$ points
• $20$ à $9$ points, $\ldots$

Voici quelques configurations obtenues pour $12$ points :

Et pour $10$ points :

Conjecture : les points semblent être cocyclique