Maintenant que nous avons nos pendules expérimentaux et théoriques, il nous est possible de les comparer.
En effet, le but final étant de répondre à la problématique : Les mathématiques peuvent-elles tout prévoir ? , nous devons mettre en parallèle les résultats attendus (théoriques) et ceux obtenus (expérimentaux).
Pour cela, il faut que les pendules théorique et expérimental aient les mêmes caractéristiques. En effet, nous avons vu que la trajectoire du système dépend de ses angles de départ, de ses vitesses angulaires initiales, etc. Commençons donc à chercher les positions des centres de gravité de nos deux bras.
Centres de gravité
Bras n°1
Le bras n°1 se compose non seulement d’une partie massive (en bois) mais également d’éléments métalliques (la visserie).
Partie massive
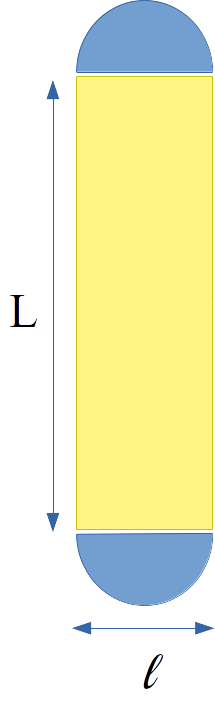
Soit $S_T$ la surface totale du bras (sans les trous), $S_R$ celle du rectangle (jaune) et $S_C$ du cercle (deux demi-cercles bleus).
On a :
$S_T = S_R + S_C$
$S_T = L\times l + \pi \times \left(\frac{l}{2}\right) ^2$

Soit $S_F$ la surface finale du bras (en tenant compte des trous), $S_{T_1}$ celle du plus grand trou et $S_{T_2}$ du plus petit.
On note $d_1$ et $d_2$ les diamètres respectifs de ces trous. On a donc :
$S_F = S_T – S_{T_1} – S_{T_2}$
$S_F =S_T – \pi \times \left(\dfrac{d_1}{2}\right)^2 – \pi \times \left(\dfrac{d_2}{2}\right)^2 $
Pour calculer la position du centre de masse, comme son nom l’indique, il nous faut connaître la masse de chaque élément. Pour l’instant, nous ne prendrons en compte que le bras lui même (on exclut les vis, roulements à billes, etc.)
Dans le cas présent, ni l’épaisseur ni la matière ne change, il y a donc une relation de proportionnalité entre la surface et la masse, relation que l’on va traduire par la masse surfacique :
$\sigma = \frac{m}{S}$ avec $m$ la masse et $S$ la surface, on a $\sigma$ constante.
On va à présent pouvoir calculer la masse des trois éléments évoqués ci-dessus : deux anneaux ($C_1$ et $C_2$) et un rectangle $R$ auquel on a soustrait un disque.
Pour commencer, calculons leurs surfaces respectives :
$S_{C_1} = S_C – S_{T_1}$
$S_{C_2} = S_C – S_{T_2}$
$S_{R} = S_R – S_{C}$
On associe maintenant à chacune de ces aires, une masse : soit $m_{C_1}$ la masse de $S_{C_1}$, $m_R$ la masse de $R$, et $m_{C_2}$ la masse de $S_{C_2}$,
$m_{C_1} = \sigma \times S_{C_1}$
$m_R = \sigma \times S_R$
$m_{C_2} = \sigma \times S_{C_2}$
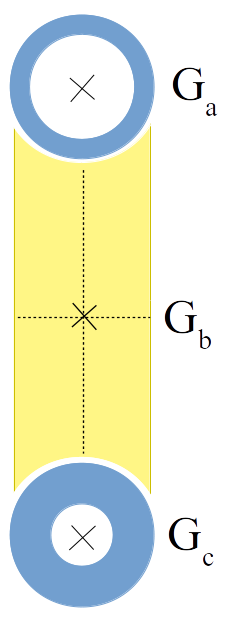
Pour calculer le centre de masse du bras, commençons par trouver celui de chacune des trois pièces :
- Soit $G_{C_1}$ le centre de masse de $S_{C_1}$, alors $G_{C_1}$ sera confondu avec le centre de l’anneau
- Soit $G_R$ le centre de masse de $S_R$, alors $G_R$ sera à la croisée des axes de symétrie du rectangle
- Soit $G_{C_2}$ le centre de masse de $S_{C_2}$, alors $G_{C_2}$ sera confondu avec le centre de l’anneau
Le centre d’inertie d’un système à plusieurs corps se calcule grâce à la formule : $\sum m_i \overrightarrow{GG_i} = \overrightarrow{0}$ avec $G$ le centre d’inertie recherché et $m_i$ et $G_i$ la masse et le centre d’inertie de chaque corps composant le système étudié.
Puisque l’on est en présence de trois corps la formule se réécrit : $m_{C_1} \overrightarrow{GG_{C_1}} + m_R \overrightarrow{GG_R} + m_{C_2} \overrightarrow{GG_{C_2}} = \overrightarrow{0}$
En appliquant la relation de Chasles on obtient :
- $\overrightarrow{GG_R} = \overrightarrow{GG_{C_1}} + \overrightarrow{G_{C_1}G_R}$
- $\overrightarrow{GG_{C_2}} = \overrightarrow{GG_{C_1}} + \overrightarrow{G_{C_1}G_{C_2}}$
Donc, $m_{C_1} \overrightarrow{GG_{C_1}} + m_R\overrightarrow{GG_{C_1}} + m_R\overrightarrow{G_{C_1}G_R} + m_{C_2}\overrightarrow{GG_{C_1}} +m_{C_2} \overrightarrow{G_{C_1}G_{C_2}} = \overrightarrow{0}$
Soit :
$\overrightarrow{GG_{C_1}}(m_{C_1} + m_R + m_{C_2}) + m_R\overrightarrow{G_{C_1}G_R} +m_{C_2} \overrightarrow{G_{C_1}G_{C_2}} = \overrightarrow{0}$
Les centres de gravité sont alignés, on peut donc passer à une écriture algébrique :
$\overline{G_{C_1}G} = \dfrac{m_R\overline{G_{C_1}G_R} +m_{C_2} \overline{G_{C_1}G_{C_2}}}{m_{C_1} + m_R + m_{C_2}}$
Puisque le premier bras mesure $150$ mm $\times$ $32$ mm, pèse $8$ g, et que ces deux trous ont un diamètre de $22$ mm et $8$ mm, on obtient $\overline{G_{C_1}G} = 80$ mm
A ceci, il faut rajouter les rondelles, vis, écrous, etc.
Visserie
Commençons par $O$, la seule pièce rajoutée est un roulement à billes et une vis.
La vis étant liée au support, on ne la compte pas. De même pour la bague intérieure du roulement puisqu’elle est directement tenue par la vis, il faut donc rajouter le poids d’un roulement à billes sans sa bague intérieure, c’est à dire $7.6$ g.
Notons qu’il a fallu, pour cette mesure, démonter un roulement à bille, ce qui n’a pas été chose facile ! de plus, tous les relevés de masse ont été effectués avec une balance Jeulin précise à 0.1g.
Maintenant pour $M_1$, il faut rajouter une rondelle, une petite vis, deux écrous, et une bague intérieure (que l’on ne comptera pas pour le deuxième bras). Ce qui correspond à $28.4$ g.
On arrive au final à une distance $\overline{G_{C_1}G} = 106.7$ mm.
Bras n°2
En procédant de la même manière avec le second bras on obtient une distance de $29.6$mm entre $G_{C_2}$ et le centre de gravité.
On peut dès lors modéliser le double pendule avec les mêmes caractéristiques que le pendule expérimental.
Ça frotte ou pas ?
Modélisation sans frottement
Nous avons créé un programme auquel on fournit les coordonnées expérimentales d’un pendule (obtenues précédemment), et à partir des mêmes conditions initiales ($\theta_1$ et $\theta_2$) il superpose un pendule théorique.
Ainsi, les deux pendules partent exactement du même endroit, avec la même vitesse initiale nulle … à peu près !!
Voici une des vidéos obtenues :
Le pendule rouge correspond au pendule expérimental et le bleu au théorique.
Dès le début, on remarque que la différence de trajectoire est très importante, on pouvait s’y attendre !
Une piste d’amélioration de la modélisation consiste à prendre en compte les frottements. En effet, bien qu’équipé de roulements à billes, le pendule est ralenti par ses frottements contrairement au théorique.
Ceci pourrait expliquer la vitesse élevée du pendule bleu par rapport au rouge. De plus, le phénomène s’accroît au cours du temps si bien que le rouge ne parvient rapidement plus à la hauteur que peut atteindre le bleu.
Essayons avec un angle initial plus petit, on devrait avoir moins de différences :
On peut renouveler les remarques précédentes, dans la mesure où les mêmes phénomènes interviennent bien qu’atténués.
En effet, l’angle initial étant plus petit, les pendules restent « assez » proches, même si le bras du pendule expérimental tourne moins vite que le théorique.
Modélisation avec frottements
Pour obtenir un résultat plus réaliste, nous avons rajouté des forces de frottement dans notre simulation.
Pour cela, il faut introduire des termes dissipatifs dans les équations. Cela revient à ajouter : $\left\{
\begin{array}{l}
\beta_1 \dot{\theta_1}\\
\beta_2( \dot{\theta_2} – \dot{\theta_1})
\end{array}
\right.$ où les $\beta_i$ sont les coefficients de frottements. Ces termes, proportionnels à la vitesse de rotation des bras (bras n°1 par rapport au bâti, et bras n°2 par rapport au bras n°1) expriment une sorte de « freinage ».
On obtient alors les équations suivantes :
$\left\{
\begin{array}{l}
(m_1 l_{g_1}^2 + m_2 l_1^2) \ddot{\theta_1} + m_2 l_1 l_{g_2} \cos(\theta_1 – \theta_2) \ddot{\theta_2} + m_2 l_1 l_{g_2} \sin(\theta_1 – \theta_2) \dot{\theta_2}^2 + (m_1 g l_{g_1} + m_2 g l_1)\sin \theta_1 + \beta_1 \dot{\theta_1}= 0\\
l_1 \cos(\theta_1 – \theta_2) \ddot{\theta_1} + l_{g_2} \ddot{\theta_2} – l_1 \sin(\theta_1 – \theta_2) \dot{\theta_1}^2 + g \sin \theta_2 + \dfrac{\beta_2}{m_2 l_{g_2}}( \dot{\theta_2} – \dot{\theta_1}) = 0
\end{array}
\right.$
Avec ces nouvelles équations nous avons complété les algorithmes permettant de comparer l’expérimental au théorique.
Pour choisir les coefficients de frottement, nous avons comparer les comportements des deux pendules vers la fin car ils doivent être freinés avec la même intensité. Vouloir les déterminer sur les premiers instants permet de faire mieux coller les trajectoires, mais au global les mouvements seront très différents. Nous avons donc opté pour un « équilibrage » global.
On obtient la vidéo suivante avec toujours en rouge le pendule expérimental et en bleu le pendule théorique :
On remarque que les deux pendules se suivent sur la première descente et toujours un peu sur la première montée, mais dès lors, leurs comportements diffèrent puisque le second bras du pendule théorique fait un tour complet tandis que l’autre non.
On pourrait être alors tenté d’augmenter les frottements du second bras ; on éviterait ainsi le tour complet donc la trajectoire correspondrait mieux à l’expérimental au début mais très vite le bras n’aurait pas assez d’énergie et s’arrêterait prématurément.
Quels que soient les coefficients choisis, les trajectoires divergent rapidement.
Bilan
C’est le temps fort de notre TPE : l’aboutissement d’une démarche scientifique visant à confronter une expérience physique à un modèle numérique.
Le résultat est très satisfaisant car nous montrons des similitudes mais l’imprécision des paramètres du modèle (masses, longueurs, coefficients de frottement, etc.) se transforme en divergence importante des trajectoires, ce qui est caractéristique des systèmes chaotiques.