Présentation
Voyons ce qu’en dit Dr Nozman :
Un double pendule n’est donc qu’un simple pendule, accroché à un autre pendule simple. Tout simplement.
Idée et dimensionnement
L’idée générale de départ a été d’utiliser un principe de « motion capture » simplifié :
- des pastilles réfléchissantes sont collées sur les points mobiles du double pendule,
- les autres parties du dispositif sont peintes en noir,
- une caméra filme le dispositif en mouvement et,
- par post-traitement numérique, on isole le mouvement des points mobiles.
Bon, ça c’est le principe de départ. Mais comment dimensionner le dispositif sans indications particulières et sans trop se tromper ? En fait … un peu au hasard avec des « ni trop » et des « ni trop peu ».
Il s’avère, par chance, que l’on n’a pas eu à retoucher notre premier prototype.
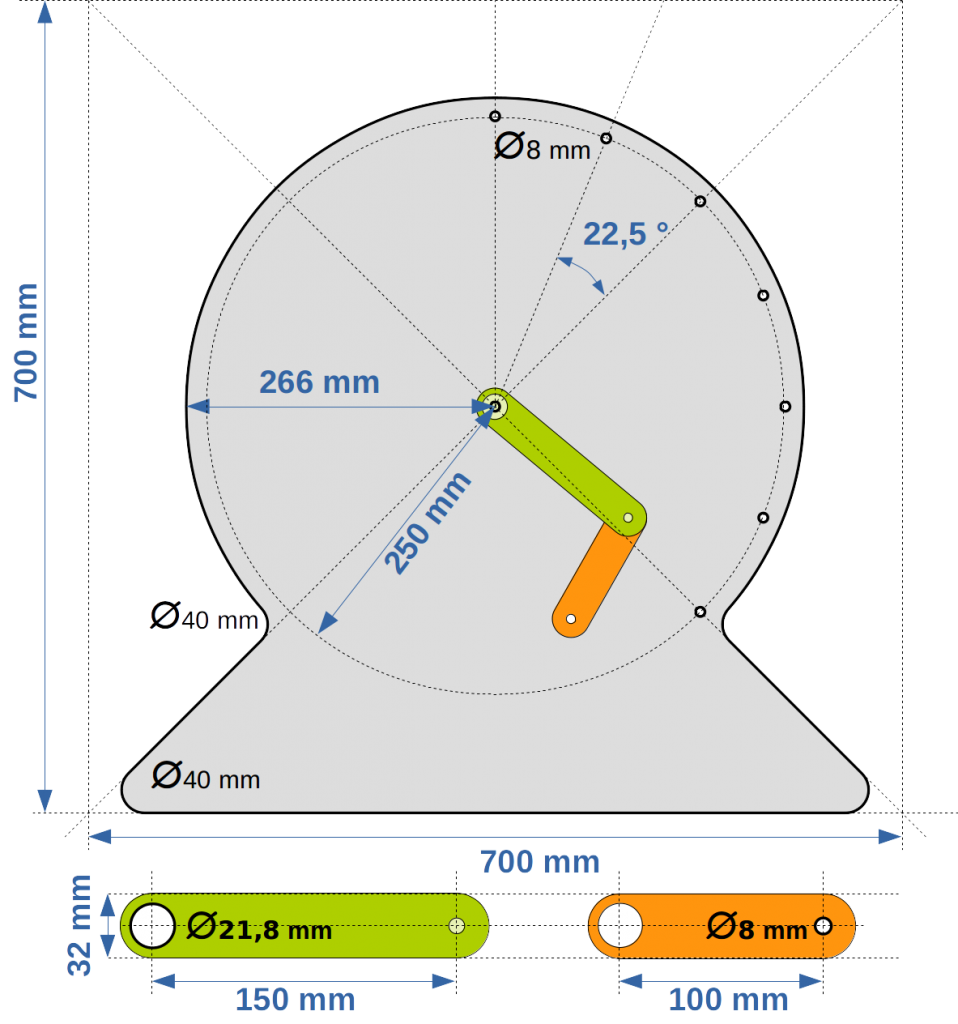
Les dessins ont été réalisés sur le logiciel libre FreeCad (création d’un fichier dxf pour la découpe laser) puis LibreOffice Draw pour l’illustration ci-contre.
Nous avons bénéficié de l’aide d’un mécanicien de formation pour la création du dessin.
Les seules contraintes que l’on a eues sont dues à la visserie et aux roulements à billes, pour le diamètre des trous.
Pour ce qui est du matériau utilisé, nous avons récupéré une grande planche de contre-plaqué de 4 mm d’épaisseur.
Réalisation
Les liaisons
Naturellement, on pense aux roulements à bille pour assurer la rotation sans frottement des bras. On va s’apercevoir que ça n’est pas si simple.
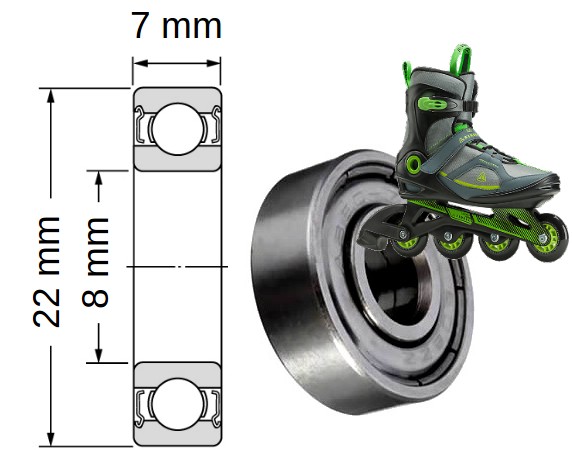
Nous avons donc acheté un jeu de roulements à billes « ABEC 7 » dans un grand magasin de sport. Ces roulements sont utilisés sur les rollers et les skateboards.
La première difficulté rencontrée a été les frottements importants dans ce type de roulements. La conséquence directe était que le double pendule n’était pas … chaotique !
On peut expliquer intuitivement ce phénomène par le fait que les mouvements étant très freinés, les amplitudes restaient faibles et le dispositif se comportait rapidement comme un pendule simple.

Nous avons donc ôté les flancs et rincé les roulements à l’essence F.
Débarrassés des flancs protecteurs et de la graisse, les roulements présentaient beaucoup moins de frottements, et le double pendule se comportait bien de façon chaotique.
Afin de limiter un peu plus encore l’effet des frottements, nous avons choisi de lester les parties mobiles avec la visserie (métallique plutôt que plastique).
L’ensemble mobile
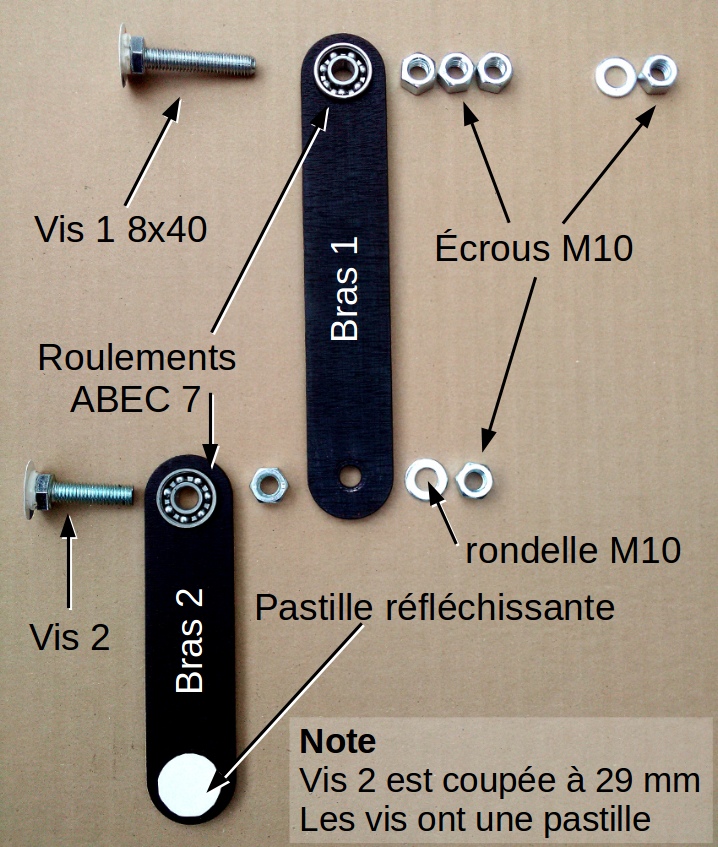
On peut voir ci-contre les différents éléments constitutifs du dispositif.
- La vis 1 est celle qui relie les parties mobiles au bâti, elle est immobilisée avec l’écrou et la rondelle (en haut à droite)
- Les trois écrous du haut servent à éloigner suffisamment les bras du bâti.
- Les roulements sont montés serrés dans les bras.
- La vis 2 a été sciée pour ne pas trop dépasser.
- Les vis ont une pastille réfléchissante (carton blanc glacé) collée avec de la patafix. Elle doivent être suffisamment grandes pour couvrir les roulements à billes.
Le bâti

Le bâti, ainsi que les deux bras, ont été découpés à l’IUT d’Angoulême au département QLiO par M. Francisco.
Le procédé utilisé est la découpe laser. Il s’agit d’une machine générant un faisceau laser de 100 W pouvant découper des épaisseur jusqu’à 10 mm. Ce type de laser (infra-rouge) de faible puissance ne permet pas de découper des pièces métalliques.
Le but étant d’isoler le signal venant des pastilles, tout a été peint en noir (peinture acrylique classique mate)
La difficulté suivante rencontrée était le faible maintien du dispositif et son manque de rigidité.
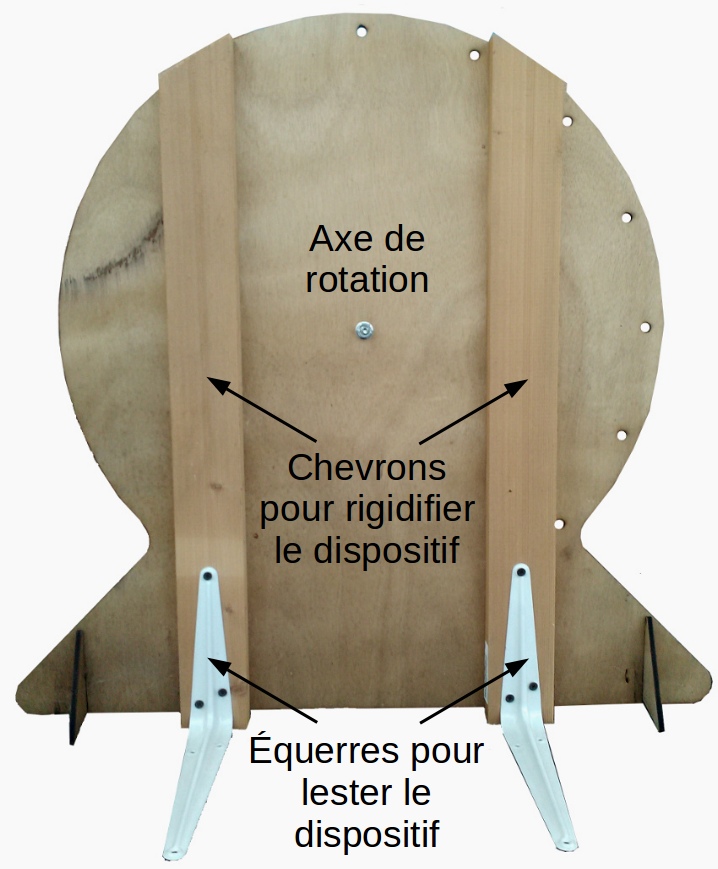
La solution apportée est très simple :
- Des chevrons épais, solidement liés au bâti.
- Des équerres pour pouvoir lester l’ensemble du dispositif avec des livres, des paquets de feuilles, etc., le jour J de l’oral du TPE.
Ça marche !
Conditions expérimentales
Prise de vue
Pour suivre l’idée de départ du « motion capture », il faut une grande vitesse d’exposition associée à un éclairage fort. En effet, le point $M_2$ se déplaçant rapidement, si l’on veut que les images soient nettes pour le post-traitement, il faut que la prise d’image soit courte mais il faut également que suffisamment de lumière soit captée.
Nous avons donc sollicité l’aide de Jean Baptiste Burn, technicien multimédia du département QLiO d’Angoulême. Après quelques tests le matériel et les réglages choisis ont été les suivants.
Matériel

Canon 7D Mark II

Objectif reflex Canon EF-S 18-135-mm f/3.5-5.6 IS-STM

Eclairage Led IDV AURORA MAX
Réglages
- Ouverture : f/3.5
- Vitesse d’exposition : 1/1600
- Iso : 100
- Résolution : 1280×720 pixels
- Fréquence d’images : 50 i/s
Traitement des vidéos
Protocole
Afin de s’assurer d’une certaine répétabilité, en gardant à l’esprit le caractère chaotique, nous avons fait plusieurs essais. Les trous à gauche du bâti sont répartis tous les $22.5°$ en partant du haut.
L’angle $0°$ étant celui du pendule au repos, le trou du haut est à $180°$. Un lâché depuis cet angle étant trop aléatoire (départ du mouvement à droite ou à gauche), nous avons pris le suivant : $180°-22.5°=157.5°$.
Un autre angle a également été choisi, au-dessus de l’horizontale, soit $135°-22.5°=112.5°$.
Nous avons donc fait cinq prises pour ces deux angles. En éliminant les prises « très différentes », il nous faut traiter huit vidéos : trois avec un angle de $157.5°$ et cinq de $112.5°$.
Afin de pouvoir comparer ces vidéos, il nous faut récupérer les coordonnées de l’axe global $O$, de l’axe mobile entre les deux bras $M_1$ et de l’extrémité $M_2$ pour pouvoir modéliser les pendules et comparer leurs trajectoires .
Moyens
A 50 images/seconde, un traitement manuel aurait été rédhibitoire. Ayant quelques compétences en Python, nous avons été orientés vers la bibliothèque OpenCV. Il s’agit d’une collection de fonctions dédiées au traitement d’image et il semble que ce soit la plus utilisée. Nous avons bénéficié de nombreux tutoriels vidéo, ce qui nous a permis de programmer les traitements adéquats.
Étapes du traitement
L’idée générale est d’isoler les pastilles du fond.
Pour cela, il faudra utiliser les traitements suivant :
- recadrage
- transformation en niveaux de gris
- histogramme des niveaux de gris
- seuillage
- érosion
- dilatation
- fermeture
- transformée de Hough
- identification des points
Images de départ

On a vu précédemment que pour obtenir une trajectoire nette et précise des extrémités des bras, on les avait marqués par des pastilles blanches et le reste avait été peint en noir.
La faible luminosité diminue le contraste entre les pastilles et le reste donc les formes ne sont pas complètement blanches ou complètement noires.
Cadrage, puis niveaux de gris
Pour permettre à un programme de trouver des formes, comme des cercles, il faut les mettre le plus possible en évidence.
Voici donc la démarche suivie pour transformer l’image (cercles blancs et fond noir) :

- L’image est d’abord cadrée, pour ne se concentrer que sur la partie utile
- Transformation de l’image en niveaux de gris : toutes les couleurs sont transformées en un gris plus ou moins foncé, en fonction de la luminosité.
- Les gris s’étalent entre la valeur 0 (noir) et la valeur 255 (blanc). Un histogramme nous aide à trouver le bon seuil pour séparer les pastilles (gris clair) du reste (gris foncé)
Seuillage, érosion, dilatation et fermeture

- Tout ce qui est en dessous d’un certain niveau de gris (le seuil) devient noir, et ce qui est au dessus devient blanc. Ainsi, on obtient une image binaire.
- Nous n’avions pas anticipé le fait qu’en dehors du cercle du bâti, des zones deviendraient blanches (il suffit de regarder en bas à gauche).
Il faut donc supprimer ces parasites.
- Pour cela, on va enlever en deux passes deux pixels autour de chaque forme : c’est l’érosion. Ainsi, les parasites disparaissent et les formes plus importantes rétrécissent.
- On ajoute ensuite deux fois deux pixels autour des formes restantes pour leur rendre leur taille d’origine : c’est la dilatation.
- Enfin, on rempli de blanc les formes aux contours fermés (les cercles seront ainsi complètement blancs, sans trous) : c’est la fermeture.
Transformée de Hough
Maintenant, le programme peut trouver des cercles (les pastilles) dans cette image très propre. Pour cela on utilise la transformée de Hough en suivant la documentation d’OpenCV car le paramétrage de cette opération est délicat. La méthode en elle-même est complexe et nous n’avons pas tout compris.

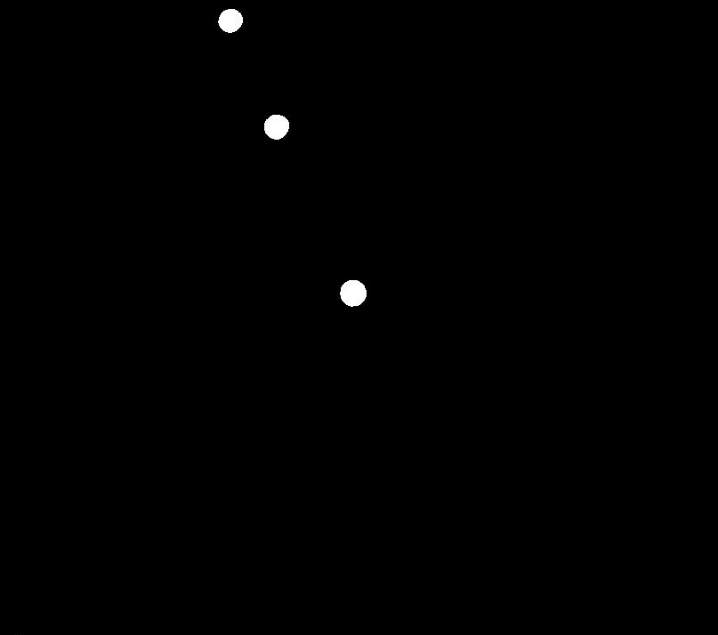
Voici une image finalement obtenue.
La transformée de Hough fournit les coordonnées des cercles détectés ainsi que leur rayon, sans ordre particulier : cette liste peut contenir d’abord $M_1$, puis $O$ et $M_2$ pour finir.
Chacune des images de la vidéo reçoit la même séquence de traitements, on peut ainsi vérifier que les cercles ont été correctement détectés.
On obtient alors la vidéo suivante :
Qui est qui ?
Le programme reçoit donc les coordonnées des cercles dans une liste, dans un ordre quelconque : on ne peut pas savoir lesquelles correspondent à quel point. Il va alors falloir créer un algorithme permettant de différencier à coup sûr les trois cercles à partir de leur coordonnées.
Pour $O$, c’est très simple : il ne bouge pas, ses coordonnées ne varieront donc pas (ou très peu).
Il ne reste qu’à différencier $M_1$ de $M_2$.
Puisque $M_1$ est directement relié à $O$ par un bras, la distance qui les sépare ne varie pas (ou peu), il suffit donc d’analyser la première image, de noter la distance $d_{ref} = OM_1$ et de la soustraire aux distances mesurées sur les prochaines images entre $O$ et les deux points inconnus : $d_i=|OM_i -d_{ref}|$
La plus petite valeur $d_i$ nous indique la position de $M_1$.
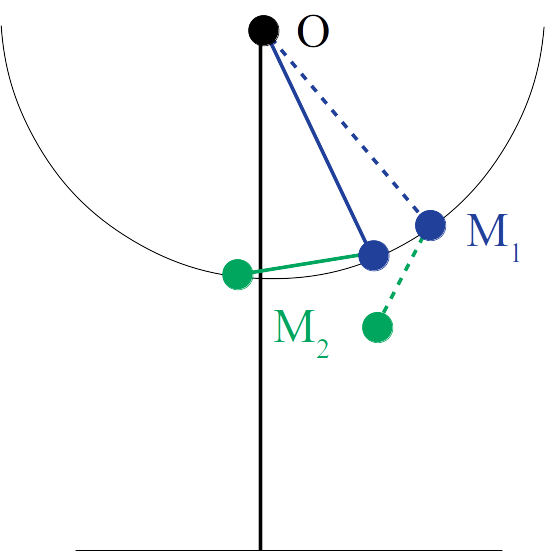
Néanmoins, il existe des cas pour lesquels $OM_1= OM_2$, alors comment différencier les deux points ?
Pour cela, on va se référer à l’image précédente (pointillés) et comparer les distances entre les points $M_{1, avant}$ et $M_{1, après}$ d’une part et $M_{2, avant}$ et $M_{2, après}$ d’autre part.
Exemple
Le point $M_{1, avant}$ (de la première image) ne pourrait pas avoir pris la position du point $M_{2, après}$ sur la seconde car la distance serait bien trop grande.
On peut ainsi, affiner le critère de discrimination précédent.
Vérifions qu’il n’y ait pas eu d’inversion dans les points :
Bilan
Maintenant que toutes les vidéos ont été traitées, il nous est possible de récupérer les coordonnées des trois points pour chaque image et donc de modéliser les pendules.
Le but étant de mettre en avant le caractère imprévisible des trajectoires, nous avons superposé dans un premier temps les trois pendules lâchés d’un angle initial de $157.5°$ :
Puis les cinq de $112.5°$ : (vitesse ralentie)
On remarque que les bras bleu et vert ainsi que rose et gris ont des trajectoires similaires au début puis s’écartent progressivement les uns des autres.
Cependant ce phénomène n’est pas très prononcé car, expérimentalement, les frottements bien que diminués sont encore importants et freinent les mouvements du pendule.
Une autre limite de l’expérimental est le départ : en effet, lorsque le pendule est lâché, il est possible qu’il ait reçu une petite quantité d’énergie. Ainsi, la vitesse angulaire initiale n’est peut-être pas exactement égale à $0$.
Avec le recul, il s’avère que nous aurions pu arriver aux mêmes résultats plus facilement. OpenCV permet la reconnaissance de formes à partir de leurs couleurs. Ainsi, avec :
- un fond rectangulaire blanc (et non pas un disque noir),
- $O$ en noir,
- $M_1$ en bleu,
- $M_2$ en rouge
on se serait économisés des traitements numériques !
Néanmoins, nous avons réalisé un double pendule et il se comporte de façon chaotique : bien que les lâchés se fassent dans les mêmes conditions, le comportement change radicalement assez vite.
Il est temps maintenant de se confronter à la théorie !