Avant de rentrer dans le vif du sujet, commençons par éclaircir quelques notions.
Définitions
Étymologiquement le mot chaos vient de « Klàos », en grec, qui signifie faille, confusion, ou désordre grave. Dans l’ancien temps, il désignait tant l’inconnu que le monde des esprits ou encore la peur de l’incontrôlable.
D’autre part, on appelle théorie toutes connaissances ou suppositions, qui tentent d’expliquer certains phénomènes.
Ainsi, la théorie du chaos serait une explication de phénomènes confus. Cette définition, bien qu’erronée, se rapproche légèrement du véritable sens de cette expression.
En réalité, la théorie du chaos est l’étude de systèmes très dépendants des conditions initiales, qui, avec le temps, deviennent imprévisibles.
Historique

Henri Poincarré peut être considéré comme l’un des précurseurs de la théorie du chaos. Célèbre mathématicien (qualifié de génie des mathématiques) mais aussi physicien, théoricien et philosophe, on lui doit les premières recherches sur la théorie du chaos.
Il a travaillé sur les systèmes chaotiques, à travers la stabilité du système solaire. A son époque, période où la science commençait peu à peu à prendre la place de la religion et où la vulgarisation scientifique devenait toute aussi importante, il ne possédait pas la technologie nécessaire pour effectuer ses calculs. Ses recherches se sont donc rapidement arrêtées.
La naissance de la théorie est principalement due aux lois newtoniennes. Celles-ci permettent de déterminer la trajectoire d’un corps à partir de l’étude de son mouvement grâce à des équations différentielles.
En mathématiques, une équation différentielle est une équation dont la ou les inconnues sont des fonctions ; elle se présente sous la forme d’une relation entre ces fonctions inconnues et leurs dérivées successives. C’est un cas particulier d’équation fonctionnelle. Wikipedia
Les lois formulées par Newton ont eu un grand succès, et nombreux sont les scientifiques qui ont voulu les appliquer aux phénomènes météorologiques. Persuadés que le hasard n’existait pas, que tout était prévisible, ils ont entrepris un long travail visant à prédire la météo dans le futur. Cette science consistant à connaître le mouvement de grandes masses d’air, il suffisait, selon eux, de traduire ces déplacements par des équations différentielles …
Ces équations étant très compliquées, les mathématiciens de l’époque ont voulu les simplifier, les « linéariser ». Ils étaient convaincus que les effets étaient proportionnels aux causes, que les « termes » compliqués ne jouaient qu’un rôle mineur, et n’affecteraient pas réellement les résultats.
Seulement, dans l’étude météorologique, de nombreux facteurs sont à prendre en compte : la différence de température entre les pôles et l’équateur, la rotation de la Terre qui engendre certains vents, les conditions au sol qui varient d’un endroit à un autre etc., enfin une multitude de facteurs. Le mouvement de n’importe quelle masse d’air dépend des mouvements de toutes les petites masses d’air qui la composent.
Il y a donc un choix à faire, établir des équations différentielles aussi précises que possible ou les simplifier au maximum, à tel point qu’elles ne pourraient plus prévoir le temps de manière exacte.

C’est à ce moment qu’intervient Edward Norton Lorenz, un scientifique passionné par les problèmes mathématiques sans solutions mais également par la météorologie, qu’il découvrit en tant que soldat, durant la guerre.
Ce dernier a opté pour la seconde solution : la compréhension aux dépens de la réussite, soit aux dépens d’une prévision exacte.

Il a donc créé un système d’équations différentielles, très simplifié, composé de seulement trois variables, permettant de déterminer l’évolution des masses d’air.
Il utilisa également un ordinateur, très différent des nôtres car nous sommes ici en 1961, qui lui permettait d’expérimenter ses idées ou encore de tester le rôle d’un paramètre.
Il s’est donc équipé d’un « Royal MC Bee LGP-300 », une machine à calcul dont les résultats sortaient, sous formes de colonnes, avec six décimales de précision.
Une journée d’hiver 1961, Lorenz avait fourni une série de données à son ordinateur, qui prit longtemps à les traiter. Lorsque ce fut fini, il décida de recommencer, afin de s’assurer de la véracité de certains résultats, en ne gardant que trois décimales au lieu de six. Persuadé que de petites incertitudes au départ ne pouvaient engendrer que de petites incertitudes à l’arrivée …
Cependant, en observant les résultats, il se rendit vite compte que quelque chose n’allait pas : au début les résultats étaient les mêmes, mais très vite ils se sont mis à diverger de façon tellement importante que les deux systèmes obtenus n’avaient plus rien à voir. Tandis que le premier indiquait une tempête au pôle Nord, le second prédisait une sécheresse sous les tropiques !
C’est ainsi que Lorenz découvrit que même dans des systèmes linéaires, d’infimes différences dans les conditions initiales engendraient de grands écarts par la suite, créant des systèmes totalement différents. Il comprit que prédire la météo de façon précise serait à jamais impossible. Cette découverte remit en cause les certitudes et prétentions de nombreux physiciens.
Certains systèmes dynamiques non linéaires sont si sensibles aux conditions initiales que, même s’ils sont régis par des lois rigoureuses et parfaitement déterministes (n’importe qu’elle condition initiale détermine entièrement l’évolution future car le hasard n’existe pas), ses prédictions exactes sont impossibles.
Image et exemples
« Effet papillon », oui, le fameux
La théorie du chaos est souvent illustrée par l’effet papillon, un principe dont on ne connait pas toujours le sens.
Pour le comprendre, revenons à la météorologie. Afin de prévoir le temps de manière précise, il faudrait connaître tous les mouvements (même les plus infimes), de toutes les masses d’air du globe. Que se soit une bourrasque, une personne qui parle ou encore un battement d’ailes de papillon. « Celui-ci, est d’autant plus important qu’il pourrait provoquer une tempête au Texas » d’après Lorenz. Il suffit de modifier de façon infime un paramètre dans un modèle météorologique pour que celui-ci s’amplifie progressivement et provoque à long terme, des changements colossaux.
Il ne faut toutefois pas exagérer : ça n’est pas en baillant que l’on va changer quoi que ce soit à la météo. A l’échelle de l’atmosphère, un bâillement ne représente « rien », ou peut-être un « petit quelque chose » dans … quelques milliers d’années.
La météo n’est pas le seul système à réagir de la sorte…
Un modèle numérique simple
Cherchons un modèle numérique simple pour illustrer l’influence des conditions initiales sur le comportement d’un système puisqu’il est fait mention plus haut de systèmes linéaires chaotiques.
Sur sa chaîne Youtube ScienceEtonnante, David Louapre traite le sujet en profondeur et montre parfaitement en quoi la fonction $f(x)=4x(1-x)$ a un comportement chaotique :
Billard
On peut aussi illustrer la théorie du chaos par le déplacement de boules de billard !
En effet pour deux tables de billard identiques, c’est-à-dire qui ont le même nombre de boules, disposées aux mêmes endroits, il suffit qu’une seule soit décalée de quelques millimètres, sur l’un des deux pour que les mouvements des boules sur chacun diffèrent complètement après un certain temps.
Une seule incertitude sur une boule rend la prévision impossible après quelques secondes : c’est la définition même d’un système chaotique.
Regardez les vidéos proposées par Etienne Ghys, c’est génial !! D’ailleurs, en voici un extrait.
Vague scélérate
Une vague scélérate est une gigantesque vague mesurant entre 20 et 30 mètres ! Elles ont longtemps été considérées comme un mythe, les marins étant connus à l’époque pour leurs alcoolisme, et donc ils perdaient toute crédibilité. En effet, parler de murs d’eau sortis de nulle part, c’est suspect !
La première preuve scientifique irrévocable, de l’existence de vague scélérate date de 1995. Ce jour-là une vague scélérate (appelée par la suite, vague du nouvel-an) a été mesurée, pour la première fois après avoir déferlé sur la plate forme pétrolière de Draupner. Elle faisait 25,6 mètres !
On peut penser que les vagues scélérates s’inscrivent dans la théorie du chaos puisque la principale cause de la formation de ces vagues est le vent et le cumul de masses d’eau liées au mouvement de l’océan. Le vent se déplaçant de zones de hautes pressions vers les zones de dépression, il créé l’apparition d’ondulations plus ou moins importantes, en fonction de sa force. Nous voici donc ramenés à des phénomènes météo.
Il faut toutefois noter que des études récentes semblent montrer la répétabilité du phénomène, ce qui le disqualifierait. On met donc dans le sac chaotique ce que l’on ne peut pas expliquer ? Non, c’est sûrement plus complexe que cela.
Un contre-exemple : le pendule simple
Présentation
Un pendule simple est une masse ponctuelle fixée à l’extrémité d’une tige rigide pouvant tourner sans frottements autour de son extrémité fixe.
Le pendule simple est parfaitement déterministe : il n’y a pas de hasard qui intervienne. On peut si bien en prévoir le mouvement, que ce système est à la base du mécanisme des horloges ! Ainsi, si on le lance avec un angle légèrement différent, on obtiendra des résultats quasiment identiques.
Imaginez : si ce système était chaotique on n’aurait pas tous la même heure 🙂
Modélisation
L’énergie mécanique $E$ d’un système étant la somme des énergies potentielle $E_p$ et cinétique $E_c$, elle s’écrit, pour le pendule simple, $E = E_p + E_c$ avec :
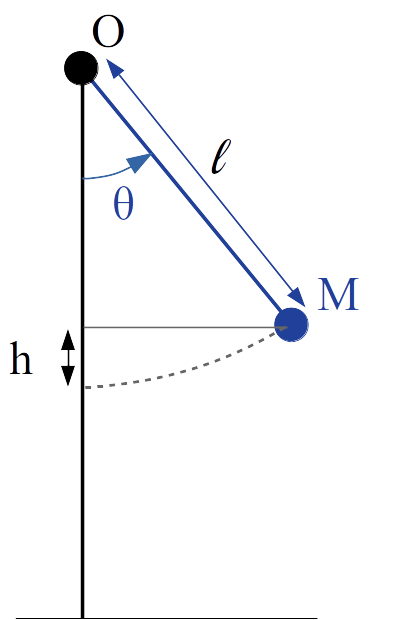
- $E_p = mgh$, $m$ étant la masse, $g$ l’accélération de la pesanteur et $h$ l’élévation du point $M$ par rapport à sa position au repos,
- $E_c = \frac{1}{2} m v^{2}$, $v$ étant la vitesse du point $M$.
Il s’agit à présent d’exprimer $h$ et $v$ en fonction de $\theta$.
Calculons $h$ :
$\cos(\theta) = \frac{l – h}{l}$ d’où $h = l(1 – \cos(\theta))$,

Et concernant $v$ :
Sur le schéma ci-contre on a $\theta (t + dt) – \theta (t) = d\theta$ et $ds = \tan(d\theta )\times l$
Or $v = \dfrac{ds}{dt}$ , d’où :
$v= \dfrac{ \tan(d \theta )}{dt} \times l$
Mais, quand $\theta$ est très petit $\tan{(\theta)} \simeq \theta$ donc :
$v = \dot \theta \times l$. On obtient finalement :
$E =\frac{1}{2} m l^{2} \dot \theta ^2 + m g l(1 – \cos\theta)$
Dans l’hypothèse où les frottements sont nuls, l’énergie mécanique ne se perd pas, $E$ est donc constante.
Exprimons le fait que $E$ soit constante, en écrivant que sa dérivée par rapport au temps est nulle :
$\dfrac{dE}{dt} = m l^2 \dot \theta \ddot \theta + m g l\dot \theta \sin{\theta} = 0$.
Puisque $\dot \theta \ne 0$ (sinon le pendule serait immobile) de même que $m$ et $l$ on a :
$$ l \ddot \theta + g \sin{\theta} = 0$$
Remarque
Étonnamment, le mouvement ne dépend pas de la masse $m$ du bras mais seulement de sa longueur $l$ (c’est-à-dire du centre de gravité à l’axe).
On cherche à présent, à exprimer $\theta$ en fonction du temps.
Solution approchée
D’après ce qui vient d’être dit :
$\ddot \theta = \dfrac{-g}{l}\sin \theta$ mais cette équation différentielle n’a pas de solution analytique.
On peut toutefois la simplifier avec une approximation :
lorsque $\theta$ est très petit, $\sin \theta \simeq \theta$. Donc, pour les petits mouvements l’équation devient : $\ddot \theta = -\dfrac{g}{l}\times \theta$
Il s’agit maintenant de trouver une fonction $f(x)$ telle que $f'{}’ (x)=\alpha f(x)$ avec $\alpha$ une constante.
Après avoir essayé plusieurs fonctions usuelles, on remarque que :
Si $f(x) = a\sin(kx + p)$, alors :
- $f'(x) = ak \times \cos(kx + p)$
- $f'{}'(x) = -ak^2 \times \sin(kx + p)$
et donc $f'{}'(x) = -k^2 \times f(x)$.
En prenant $k = \sqrt{\frac{g}{l}}$ on peut écrire : $\theta (t)= \alpha \sin(\sqrt{\frac{g}{l}} \times t + \beta)$
Il reste à déterminer $\alpha$ et $\beta$ grâce aux conditions initiales : on a deux inconnues et deux conditions initiales (un certain angle de départ et une vitesse de départ nulle).
A $t = 0$ :
- $\theta_0 = \alpha \sin \beta$
- $\dot \theta_0 = 0$ donc $\sqrt{\frac{g}{l}} \times \alpha \cos \beta = 0$
- soit $\alpha = 0$ et donc $\theta (t) = 0$ pour tout $t$ : le pendule est au repos
- soit $\cos \beta = 0$ donc $\beta = \frac{\pi}{2}$ (modulo $\pi$ )
Pour des raisons de signe, $\beta = \frac{\pi}{2}$, et donc $\alpha = \theta_0$.
On obtient finalement :
$$\theta (t) = \theta_0 \times \sin(\sqrt{\frac{g}{l}} t + \frac{\pi}{2})$$
Modélisation numérique
Pour la programmation nous avons utilisé le langage Python, la distribution Anaconda et l’éditeur Spyder.
Nous avons d’abord simulé un pendule simple à l’aide de l’équation précédemment obtenue :
On remarque que la trajectoire du pendule est périodique, en effet dans l’animation, le pendule retrouve sa position initiale toutes les 2 secondes environ, ce que l’on confirme avec la formule approchée de $\theta$ en fonction de $t$. En effet, pour que $\sqrt{\frac{g}{l}} \delta t=2\pi$ il faut $\delta t=2\pi / \sqrt{\frac{g}{l}}$.
En prenant, $l=1$m, on obtient bien 2 s environ.
On peut donc facilement prévoir la position du pendule à un instant donné.
Maintenant que se passe t-il si on lance deux pendules dont les angles initiaux diffèrent d’un degré seulement ?
L’une comme l’autre, les trajectoires des pendules sont prévisibles. Il faut de même remarquer qu’elles sont à quelque chose près similaires.
En effet, les deux pendules semblent se suivre. Ainsi, de petites imprécisions dans les conditions initiales n’entraînent que de petites conséquences.
On peut alors en conclure que le pendule simple est bien un système déterministe, et absolument pas chaotique.
Bilan
On a montré un système mathématique très simple et chaotique, et à l’inverse un système mécanique très répandu déterministe. La différence entre les deux réside dans leur dépendance aux conditions aux limites : faible, dans le cas déterministe, et forte, pour un système chaotique.
Et si on ajoutait à notre pendule, un deuxième pendule ? La complexité augmentée du système le rendrait-il chaotique ?