Introduction
Le but de cette partie est double. D’abord nous voulions nous confronter à des équations résultant de modélisations pour voir à quel point les modèles collent, ou pas, à la réalité. D’autre part, nous voulions découvrir des aspects mécaniques et mathématiques qui ne sont pas encore au programme.
Modélisation
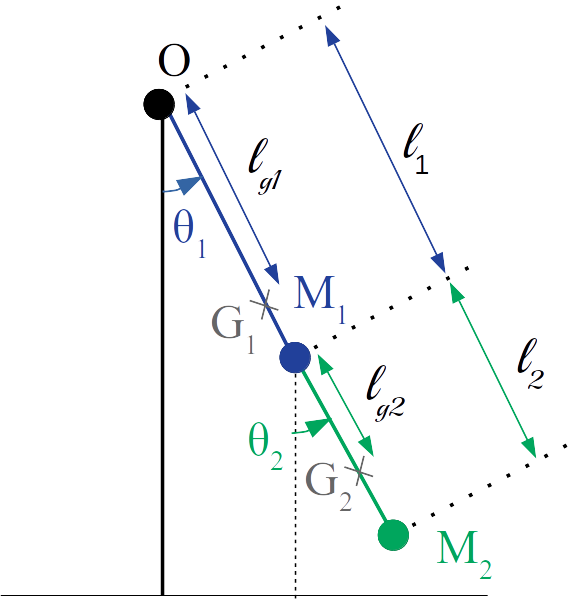
Bien que le dispositif soit simple, les équations du mouvement se compliquent par rapport à celles du pendule simple.
Les notations utilisées dans les équations qui suivent sont celles du schéma ci-contre.
On note $G_1$ et $G_2$ les centres de gravités des premier et deuxième bras, ainsi que $m_1$ et $m_2$ leurs masses respectives.
Energies mécanique et potentielle
Nous allons décomposer l’énergie mécanique du système. En effet, l’énergie mécanique d’un système est égale à la somme des énergies mécaniques des éléments qui le composent.
Pour chaque composant, nous allons écrire l’énergie mécanique en fonction de $\theta_1$ et $\theta_2$, comme la somme de l’énergie cinétique et de l’énergie potentielle (doc).
L’énergie cinétique est l’énergie acquise par un système grâce à sa vitesse et l’énergie potentielle, un réservoir d’énergie dû, ici, à la pesanteur. Ainsi, lorsqu’on lâche un système d’une hauteur $h$ avec une vitesse $v$ initiale nulle, son énergie cinétique est initialement minimale et son énergie potentielle maximale. Lorsqu’il arrive au sol, le système a une énergie cinétique maximale et potentielle minimale : l’énergie potentielle a été transformée en énergie cinétique, il y a eu transfert.
S’il n’y a pas de dissipation énergétique durant le transfert (frottements qui génèrent de la chaleur) l’énergie mécanique $E$ comme somme des énergies cinétique $E_c$ et potentielle $E_p$ se conserve.
Bras n°1 – $OM_1$
On suppose que la masse du bras 1 est concentrée en son centre de gravité $G_1$.

$l_{g_1}$ est la distance entre $O$ et le centre de gravité du premier bras $G_1$.
$h_1$ est la hauteur du point $G_1$ telle qu’elle est indiquée sur le schéma ci-contre. $h_1$ est donc l’élévation de $G_1$ par rapport à sa position au repos.
$v_1$ est la vitesse de $G_1$, contraint de se déplacer dans un mouvement circulaire de centre $O$ et de rayon $l_{g_1}$.
On a alors $h_1 = l_{g_1}(1-\cos \theta_1)$ et $v_1 = l_{g_1} \dot{ \theta_1}$. Ce qui nous donne :
$\left\{
\begin{array}{l}
E_{p_1} = m_1gl_{g_1}(1 – \cos\theta_1)\\
E_{c_1} = \frac{1}{2} m_1 l_{g_1}^2 \dot{\theta_1}^2
\end{array}
\right.$
Bras n°2 – $M_1 M_2$

$l_{g_2}$ est la distance entre $M_1$ et le centre de gravité du deuxième bras $G_2$.
$h_2$ est l’élévation du point $G_2$ par rapport à sa position, lorsque le système est au repos. On obtient facilement :
$h_2 = l_1 (1-\cos\theta_1) + l_{g_2}(1-cos\theta_2)$
Pour calculer $v_2$, la vitesse de $G_2$, on peut dériver ses coordonnées par rapport au temps $t$, comme le montre l’illustration suivante.

Examinons le schéma ci-contre :
pour déterminer la vitesse $v_M$ de $M$ entre les instants $t$ et $t + dt$, il suffit de diviser $dl$ par $dt$.
Donc :
$v_M = \dfrac{\sqrt{dx^2 + dy^2}}{dt}$, ou encore :
$v_M = \sqrt{vx_M^2 + vy_M^2}$, avec
$\left\{
\begin{array}{l}
vx_M = \dfrac{dx}{dt}\\
vy_M = \dfrac{dy}{dt}
\end{array}
\right.$
Déterminons donc les coordonnées $(x_2,y_2)$ du point $G_2$ par rapport à $O$, puis leurs dérivées par rapport à $t$.

$\left\{
\begin{array}{l}
x_2 = l_1\sin \theta_1 + l_{g_2}\sin \theta_2\\
y_2 = l_1\cos \theta_1 + l_{g_2}\cos \theta_2
\end{array}
\right.$
$\left\{
\begin{array}{l}
vx_2 = \dfrac{dx_2}{dt} = l_1\cos \theta_1 \dot{\theta_1} +l_{g_2}\cos \theta_2 \dot{\theta_2}\\
vy_2= \dfrac{dy_2}{dt} = -l_1\sin \theta_1 \dot{\theta_1} -l_{g_2}\sin \theta_2 \dot{\theta_2}
\end{array}
\right.$, d’où après simplification :
$v_2^2 =l_1^2\dot{\theta_1}^2+ l_{g_2}^2 \dot{\theta_2}^2 + 2l_1l_{g_2} \dot{\theta_1} \dot{\theta_2} \cos(\theta_1 – \theta_2) $
Finalement :
$\left\{
\begin{array}{l}
E_{p_2} = m_2g \left[ l_1(1 – \cos \theta_1)+ l_{g_2} (1 – \cos \theta_2) \right] \\
E_{c_2} = \frac{1}{2}m_2 (l_1^2\dot{\theta_1}^2+ l_{g_2}^2 \dot{\theta_2}^2 + 2l_1l_{g_2} \dot{\theta_1} \dot{\theta_2} \cos(\theta_1 – \theta_2) )
\end{array}
\right.$
Bilan pour le système
$\left\{
\begin{array}{l}
E_{p} = m_1 g l_{g_1}(1 – \cos\theta_1) +m_2g \left[ l_1(1 – \cos \theta_1) + l_{g_2} (1 – \cos \theta_2) \right] \\
E_{c} = \frac{1}{2} m_1 l_{g_1}^2 \dot{\theta_1}^2 + \frac{1}{2} m_2 \left[ l_1^2\dot{\theta_1}^2+ l_{g_2}^2 \dot{\theta_2}^2 + 2l_1l_{g_2} \dot{\theta_1} \dot{\theta_2} \cos(\theta_1 – \theta_2) \right]
\end{array}
\right.$
On pourrait, comme pour le pendule simple, calculer l’énergie mécanique, la dériver par rapport au temps et obtenir l’équation du mouvement (conservation de l’énergie mécanique), mais non.
Le mouvement du double pendule implique deux inconnues indépendantes, $\theta_1$ et $\theta_2$ ; une seule équation ne permettrait pas de les déterminer.
Obtenir un système de deux équations à deux inconnues, de cette façon, nécessite une approche bien plus complexe.
Pour remédier à ce problème, on utilise le principe de moindre action.
Le principe de moindre action
Selon ce principe, les trajectoires de $\theta_1$ et $\theta_2$ minimisent la valeur moyenne du lagrangien $L = E_c – E_p$, soit plus formellement l’action, définie ainsi par Lagrange :
$$
\mathcal{A}(\theta(t);t_1, t_2, \theta)=\int_{t_1}^{t_2} L(t, \theta(t), \dot{\theta}(t))dt
$$
avec $L(t, \theta, \dot{\theta})=E_c – E_p$ et $\theta=(\theta_1, \theta_2)$
Ceci se traduit ici par deux relations :
$$
\left\{
\begin{array}{l}
\dfrac{d}{dt} \dfrac{\partial L}{\partial \dot { \theta_1}} = \dfrac{\partial L}{\partial \theta_1}\\
\dfrac{d}{dt} \dfrac{\partial L}{\partial \dot { \theta_2}} = \dfrac{\partial L}{\partial \theta_2}
\end{array}
\right.
$$
appelées communément « équations de Lagrange ».
Il suffit donc de déterminer $L$ ainsi que ses dérivées partielles par rapport à $\theta_1$, $\dot{\theta_1}$, $\theta_2$ et $\dot{\theta_2}$.
Équations du mouvement
\begin{equation}
\begin{aligned}
L = & \frac{1}{2} m_1 l_{g_1}^2 \dot{\theta_1}^2 + \frac{1}{2} m_2 \left[ l_1^2\dot{\theta_1}^2+ l_{g_2}^2 \dot{\theta_2}^2 + 2l_1l_{g_2} \dot{\theta_1} \dot{\theta_2} \cos(\theta_1 – \theta_2) \right]\\
& – m_1 g l_{g_1}(1 – \cos\theta_1) -m_2g \left[ l_1(1 – \cos \theta_1) + l_{g_2} (1 – \cos \theta_2) \right]
\end{aligned}
\end{equation}
$\dfrac{\partial L}{\partial \theta_1} = -m_2 l_1 l_{g_2} \dot{\theta_1} \dot{\theta_2} \sin(\theta_1 – \theta_2) – m_1g l_{g_1} \sin \theta_1 – m_2 g l_1 \sin \theta_1$
$\dfrac{\partial L}{\partial \theta_2} = m_2 l_1 l_{g_2} \dot{\theta_1} \dot{\theta_2} \sin(\theta_1 – \theta_2) – m_2 g l_{g_2} \sin \theta_2$
$\dfrac{\partial L}{\partial \dot{\theta_1}} = m_1 l_{g_1}^2 \dot{\theta_1} + m_2 l_{1}^2 \dot{\theta_1} + m_2 l_1 l_{g_2} \dot{\theta_2} \cos(\theta_1 – \theta_2)$
$\dfrac{\partial L}{\partial \dot{\theta_2}} = m_2 l_{g_2}^2 \dot{\theta_2} +m_2 l_1 l_{g_2} \dot{\theta_1} \cos(\theta_1 – \theta_2)$
$\dfrac{d}{dt}\dfrac{\partial L}{\partial \dot { \theta_1}} =m_1 l_{g_1}^2 \ddot{\theta_1}+ m_2 l_1^2 \ddot{\theta_1} + m_2 l_1 l_{g_2} \ddot{\theta_2} \cos(\theta_1 – \theta_2) – m_2 l_1 l_{g_2} \dot{\theta_2} \sin(\theta_1 – \theta_2)(\dot{\theta_1} – \dot{\theta_2})$
$\dfrac{d}{dt}\dfrac{\partial L}{\partial \dot { \theta_2}} =m_2 l_{g_2}^2 \ddot{\theta_2} + m_2 l_1 l_{g_2} \ddot{\theta_1} \cos(\theta_1 – \theta_2) – m_2 l_1 l_{g_2} \dot{\theta_1} \sin(\theta_1 – \theta_2)(\dot{\theta_1} – \dot{\theta_2})$
Écrivons maintenant la première relation $\dfrac{d}{dt}\dfrac{\partial L}{\partial \dot { \theta_1}} – \dfrac{\partial L}{\partial \theta_1} = 0$ :
$(m_1 l_{g_1}^2 + m_2 l_1^2) \ddot{\theta_1} + m_2 l_1 l_{g_2} \cos(\theta_1 – \theta_2) \ddot{\theta_2} + m_2 l_1 l_{g_2} \sin(\theta_1 – \theta_2) \dot{\theta_2}^2 + (m_1 g l_{g_1} + m_2 g l_1)\sin \theta_1 = 0$
De même la deuxième $\dfrac{d}{dt}\dfrac{\partial L}{\partial \dot { \theta_2}} – \dfrac{\partial L}{\partial \theta_2} = 0$ :
$l_1 l_{g_2} \cos(\theta_1 – \theta_2) \ddot{\theta_1} + l_{g_2}^2 \ddot{\theta_2} – l_1 l_{g_2} \sin(\theta_1 – \theta_2) \dot{\theta_1}^2 + g l_{g_2} \sin \theta_2 = 0$
On obtient donc bien deux équations du mouvement :
$\left\{
\begin{array}{l}
(m_1 l_{g_1}^2 + m_2 l_1^2) \ddot{\theta_1} + m_2 l_1 l_{g_2} \cos(\theta_1 – \theta_2) \ddot{\theta_2} + m_2 l_1 l_{g_2} \sin(\theta_1 – \theta_2) \dot{\theta_2}^2 + (m_1 g l_{g_1} + m_2 g l_1)\sin \theta_1 = 0\\
l_1 \cos(\theta_1 – \theta_2) \ddot{\theta_1} + l_{g_2} \ddot{\theta_2} – l_1 \sin(\theta_1 – \theta_2) \dot{\theta_1}^2 + g \sin \theta_2 = 0
\end{array}
\right.$
On pose :
$e_{11} = m_1 l_{g_1}^2 + m_2 l_1^2\\
e_{12} = m_2 l_1 l_{g_2} \cos(\theta_1 – \theta_2) \\
e_{13} = -(m_2 l_1 l_{g_2} \sin(\theta_1 – \theta_2) \dot{\theta_2}^2 + (m_1 g l_{g_1} + m_2 g l_1)\sin \theta_1 ) \\
e_{21} = l_1 \cos(\theta_1 – \theta_2) \\
e_{22} = l_{g_2} \\
e_{23} = -( – l_1 \sin(\theta_1 – \theta_2) \dot{\theta_1}^2 + g \sin \theta_2) \\
e_{00} = e_{11} e_{22} – e_{12} e_{21} $
Après résolution du système $2 \times 2$ en $(\ddot{\theta_1},\ddot{\theta_2})$, on obtient :
$\left\{
\begin{array}{l}
\ddot{\theta 1} = \dfrac{(e_{13} e_{22} – e_{23} e_{12})}{e_{00}}\\
\ddot{\theta 2} = -\dfrac{(e_{13} e_{21} – e_{23} e_{11})}{e_{00}}
\end{array}
\right.$
Comme pour le pendule simple, ces équations différentielles ne possèdent pas de solution analytique, mais à l’inverse, on ne connaît pas d’approximations permettant d’obtenir un résultat qui s’en rapproche.
On ne peut donc les résoudre que numériquement, c’est-à-dire par programmation.
Python étant notre langage de prédilection (en fait le seul !), on va utiliser sa fonction odeint, du paquet « integrate », lui-même inclus dans « scipy ». odeint permet de résoudre des systèmes d’équations différentielles en suivant le principe suivant :
Connaissant $(\theta_1, \theta_2, \dot\theta_1, \dot\theta_2)$ à $t=0$ d’une part et, d’autre part, $(\ddot\theta_1, \ddot\theta_2)$ en fonction de $(\theta_1, \theta_2, \dot\theta_1, \dot\theta_2)$ à tout instant, on peut de proche en proche calculer $(\theta_1, \theta_2, \dot\theta_1, \dot\theta_2)$ pour chaque instant.
Exploitation
Comme pour le pendule simple nous en avons simulé un avec les équations du mouvement obtenues :
On voit bien que le pendule ne suit pas de trajectoire cyclique comme pouvait le faire le pendule simple, en effet, aucune répétition, aucune boucle ne semble régir sa trajectoire.
D’autre part, qu’observe-t-on lorsqu’on lance trois doubles pendules dont les angles initiaux varient très peu ? Prenons par exemple $112°, 112.5°$ et $113°$.
Cette animation met en lumière la dépendance du double pendule aux conditions initiales. En effet, les trois pendules partent avec une différence d’angle minime mais, avec le temps, celle-ci augmente de sorte que les trajectoires n’ont finalement plus rien en commun.
De petites imprécisions dans les conditions initiales peuvent engendrer de grandes différences de trajectoires.
Bilan
Bien que nécessitant une mise à niveau préalable en mathématiques et mécanique, les équations du mouvement du double pendule ne sont pas si difficiles à obtenir. Le concept de lagrangien est un peu obscur mais son utilisation (pour obtenir les équations lagrangiennes du mouvement) est assez simple.
Grâce aux programmes Python de ScienceEtonnante, nous avons assez rapidement obtenu un modèle numérique du double pendule. Nous avons pu mesurer à quel point les trajectoires diffèrent avec de petits écarts sur les conditions initiales.
Il nous reste à comparer notre modèle numérique aux relevés expérimentaux. Le double pendule étant un système chaotique, nous nous attendons à de grandes différences de comportements mais logiquement, sur les tout premiers instants du lâché, les deux modèles devraient se superposer.